Análise de dados do PowderyMildew:

Introdução

O banco de dados analisado neste trabalho refere-se aos resultados de um experimento conduzido com o objetivo de avaliar o desenvolvimento do oídio (Leveillula taurica) na cultura do tomateiro sob diferentes condições de irrigação e umidade do solo.

Foram avaliadas cinco estratégias de irrigação combinadas com dois níveis de umidade do solo (alta e moderada), totalizando diferentes condições experimentais, embora o delineamento não tenha sido fatorial completo. O experimento incluiu o monitoramento da severidade da doença ao longo do tempo (0, 7, 14, 21, 28, 35, 42, 49, 56 e 63). A partir desses dados, buscou-se compreender de que forma o ambiente de cultivo, especialmente as práticas de irrigação podem influenciar a severidade do oídio.

Objetivo geral

Por meio da análise dos dados, objetivou-se avaliar a influência de diferentes sistemas de irrigação e níveis de umidade do solo sobre a severidade do oídio (Leveillula taurica) em tomateiro cultivado em sistema orgânico, considerando o progresso da doença ao longo do tempo.

Objetivos específicos

Analisar a dinâmica da severidade do oídio em diferentes combinações de irrigação e umidade do solo, ao longo do tempo;
Identificar quais estratégias de irrigação contribuem para a redução da severidade da doença;
Verificar a interação entre tipo de irrigação e nível de umidade na progressão do oídio.

Hipóteses testadas

Efeito do tipo de irrigação
- Hipótese nula (H₀₁):
  - Não há diferença significativa na severidade da doença entre os diferentes tipos de irrigação;
- Hipótese alternativa (H₁₁):
  - Pelo menos um tipo de irrigação resulta em severidade significativamente diferente dos demais.
Efeito do nível de umidade do solo
- Hipótese nula (H₀₂):
  - Não há diferença significativa na severidade da doença entre os níveis de umidade do solo;
- Hipótese alternativa (H₁₂):
  - Pelo menos um nível de umidade resulta em severidade significativamente diferente dos demais.
Interação entre tipo de irrigação e umidade do solo
- Hipótese nula (H₀₃):
  - Não há interação entre tipo de irrigação e nível de umidade. O efeito de um fator é independente do outro;
- Hipótese alternativa (H₁₃):
  - Existe interação entre os fatores, ou seja, o efeito de um tipo de irrigação depende do nível de umidade do solo.

Análise da variável resposta (Severidade do oídio)

Carregamento automático de pacotes

A primeira etapa para a análise dos dados é a instalação e o carregamento dos pacotes e dados no ambiente R.

# Instalar e carregar pacotes
#Verificação e instalação automática de pacotes necessários
packages <- c("readxl", "dplyr", "ggplot2", "epifitter", "agricolae", "car", "gganimate", "animate", "DHARMa", "ggthemes", "skimr", "DataExplorer", "tidyverse", "gifski", "showtext", "sysfonts","png", "easystats", "performance", "emmeans", "multcomp")
new_packages <- packages[!(packages %in% installed.packages()[, "Package"])]
if(length(new_packages)) install.packages(new_packages)


# Carregar os pacotes
library(readxl)
library(dplyr)
library(ggplot2)
library(epifitter)
library(agricolae)
library(car)  # para Levene
library(gganimate)
library(animate)
library(DHARMa)
library(skimr)
library(DataExplorer)
library(ggthemes)
library(tidyverse)
library(gifski)
library(showtext) #Para utilizar outras fontes
library(sysfonts) #Para utilizar outras fontes
library(png)
library(easystats)
library(performance)
library(emmeans)
library(multcomp)

Importação dos dados

Como os dados de severidade estão localizados em uma planilha do Excel, para realizar a importação dos dados necessitou-se utilizar a função read_excel( ) do pacote readxl. O data frame foi atribuído ao objeto denominado dados.

dados <- read_excel("dados.xlsx")

dados

# A tibble: 240 × 5
   irrigation_type moisture      block  time   sev
   <chr>           <chr>         <dbl> <dbl> <dbl>
 1 Drip            High moisture     1     0 0.011
 2 Drip            High moisture     2     0 0.011
 3 Drip            High moisture     3     0 0.011
 4 Drip            High moisture     1     7 0.034
 5 Drip            High moisture     2     7 0.04 
 6 Drip            High moisture     3     7 0.036
 7 Drip            High moisture     1    14 0.114
 8 Drip            High moisture     2    14 0.109
 9 Drip            High moisture     3    14 0.097
10 Drip            High moisture     1    21 0.126
# ℹ 230 more rows

Verificação do conjunto de dados

Para realizar uma inspeção inicial dos dados, foram utilizadas três funções principais no R: glimpse(), skim() e names().

A função glimpse mostra do pacote dplyr, permite uma visão geral compacta do conjunto de dados. Ela exibe:

O número de linhas e colunas;
O tipo de dado de cada variável (por exemplo, numérico, caracterer);
Os primeiros valores presentes em cada coluna;

A função skim(), do pacote skimr fornece um resumo estatístico mais detalhado. Inclui média, mediana, mínimo, máximo, número de valores ausentes (NA).

A função names() foi empregada para listar os nomes reais das colunas do dataframe, permitindo identificar com clareza as variáveis disponíveis para análise.

glimpse(dados)

Rows: 240
Columns: 5
$ irrigation_type <chr> "Drip", "Drip", "Drip", "Drip", "Drip", "Drip", "Drip"…
$ moisture        <chr> "High moisture", "High moisture", "High moisture", "Hi…
$ block           <dbl> 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, …
$ time            <dbl> 0, 0, 0, 7, 7, 7, 14, 14, 14, 21, 21, 21, 28, 28, 28, …
$ sev             <dbl> 0.011, 0.011, 0.011, 0.034, 0.040, 0.036, 0.114, 0.109…

skim(dados)

Data summary
Name	dados
Number of rows	240
Number of columns	5
_______________________
Column type frequency:
character	2
numeric	3
________________________
Group variables	None

Variable type: character

skim_variable	n_missing	complete_rate	min	max	empty	n_unique	whitespace
irrigation_type	0	1	2	15	0	5	0
moisture	0	1	13	17	0	2	0

Variable type: numeric

skim_variable	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
block	1	2.00	0.82	1	1.00	2.0	3.00	3.00	▇▁▇▁▇
time	1	31.50	20.15	0	14.00	31.5	49.00	63.00	▇▇▇▇▇
sev	1	0.13	0.12	0	0.03	0.1	0.15	0.46	▇▅▁▁▂

names(dados)

[1] "irrigation_type" "moisture"        "block"           "time"           
[5] "sev"

Estabelecendo o visual do trabalho

Estabelecendo fontes

Para aprimorar a estética visual de gráficos e aplicações no R, foram adicionadas fontes do Google Fonts utilizando a função font_add_google() da biblioteca showtext. Cada chamada da função carrega uma fonte específica, associando-a a um nome de família que pode ser usado posteriormente em elementos gráficos, como títulos, eixos e textos.

As fontes adicionadas foram: Inter, Manrope, Nunito, Work Sans, Lexend, Raleway, Quicksand, Roboto e Poppins.
Após a adição das fontes, a função showtext_auto() foi ativada. Essa função garante que as fontes personalizadas sejam corretamente renderizadas em gráficos gerados com o R, inclusive ao exportar para imagens.

font_add_google(name = "inter", family = "inter")
font_add_google(name = "manrope", family = "manrope")
font_add_google(name = "nunito", family = "nunito")
font_add_google(name = "work sans", family = "work sans")
font_add_google(name = "lexend", family = "lexend")
font_add_google(name = "raleway", family = "raleway")
font_add_google(name = "quicksand", family = "quicksand")
font_add_google(name = "roboto", family = "roboto")
font_add_google(name = "poppins", family = "poppins")
showtext_auto()

Estabelecendo cores

O vetor cores_irrigation define um conjunto de cores associadas a diferentes métodos de irrigação, permitindo a padronização visual em gráficos.

Cada tipo de irrigação é representado por uma cor específica, facilitando a visualização dos dados:

Drip: representado pela cor azul ecuro (#000194);
Furrow: verde vibrante (#28C800);
MS: vermelho intenso (#C90A00);
MS above canopy: laranja (#E68A2E);
Overhead: amarelo brilhante (#FFDE00);

cores_irrigation <- c(
  "Drip" = "#000194",
  "Furrow" = "#28C800",
  "MS" = "#C90A00",
  "MS above canopy" = "#E68A2E",
  "Overhead" = "#FFDE00"
)

cores_contorno <- c(
  "Drip" = "#000060",
  "Furrow" = "#1E9E00",
  "MS" = "#990700",
  "MS above canopy" = "#A6601F",
  "Overhead" = "#CCA800"
)

Análise exploratória dos dados

Na etapa inicial da análise exploratória, foi utilizada a função plot_missing() do pacote DataExplorer, que gera um gráfico indicando a porcentagem de dados faltantes (valores NA) por variável no conjunto de dados. Essa visualização permite identificar rapidamente colunas com dados faltantes, facilitando decisões sobre as análises subsequentes.

plot_missing(dados)

A função summary() é uma ferramenta prática para explorar rapidamente os dados. É usada para gerar um resumo estatístico básico de um data frame. Fornece medidas como mínimo, máximo, média, mediana e quartis para variáveis numéricas, e a frequência para variáveis categóricas.

summary(dados)

 irrigation_type      moisture             block        time     
 Length:240         Length:240         Min.   :1   Min.   : 0.0  
 Class :character   Class :character   1st Qu.:1   1st Qu.:14.0  
 Mode  :character   Mode  :character   Median :2   Median :31.5  
                                       Mean   :2   Mean   :31.5  
                                       3rd Qu.:3   3rd Qu.:49.0  
                                       Max.   :3   Max.   :63.0  
      sev         
 Min.   :0.00300  
 1st Qu.:0.03275  
 Median :0.09700  
 Mean   :0.12710  
 3rd Qu.:0.15025  
 Max.   :0.45700

Organização dos dados

Ao examinar os dados, observou-se que os tratamentos (irrigation_type: Drip, MS, Furrow, MS Above canopy, Overhead) não estão igualmente distribuídos entre as duas condições de umidade (moisture: high e moderate). Dessa forma para a análise visual dos dados resolveu-se dividi-los de acordo com seus níveis de umidade.

# Subconjunto para irrigação com umidade moderada
dados_moderate <- dados %>% filter(moisture == "Moderate moisture")

# Subconjunto para irrigação com umidade alta
dados_high <- dados %>% filter(moisture == "High moisture")

dados_moderate

# A tibble: 120 × 5
   irrigation_type moisture          block  time   sev
   <chr>           <chr>             <dbl> <dbl> <dbl>
 1 MS              Moderate moisture     1     0 0.009
 2 MS              Moderate moisture     2     0 0.009
 3 MS              Moderate moisture     3     0 0.009
 4 MS              Moderate moisture     1     7 0.028
 5 MS              Moderate moisture     2     7 0.025
 6 MS              Moderate moisture     3     7 0.021
 7 MS              Moderate moisture     1    14 0.077
 8 MS              Moderate moisture     2    14 0.08 
 9 MS              Moderate moisture     3    14 0.071
10 MS              Moderate moisture     1    21 0.056
# ℹ 110 more rows

dados_high

# A tibble: 120 × 5
   irrigation_type moisture      block  time   sev
   <chr>           <chr>         <dbl> <dbl> <dbl>
 1 Drip            High moisture     1     0 0.011
 2 Drip            High moisture     2     0 0.011
 3 Drip            High moisture     3     0 0.011
 4 Drip            High moisture     1     7 0.034
 5 Drip            High moisture     2     7 0.04 
 6 Drip            High moisture     3     7 0.036
 7 Drip            High moisture     1    14 0.114
 8 Drip            High moisture     2    14 0.109
 9 Drip            High moisture     3    14 0.097
10 Drip            High moisture     1    21 0.126
# ℹ 110 more rows

Análise visual

Usando o pacote ggplot2, foi explorado visualmente, por meio de diferentes gráficos, os dados de severidade da doença.

Gráficos de pontos

Nesta análise, foram desenvolvidos dois gráficos de dispersão. Esses gráficos de pontos fornecem uma visão clara da distribuição da severidade da doença ao longo do tempo, permitindo comparar como os diferentes tipos de irrigação influenciam os resultados sob distintas condições de umidade.

Gráfico de Severidade ao Longo do Tempo – Umidade Moderada

Para o conjunto dados_moderate, foi utilizado o tempo (time) no eixo X e a severidade da doença (sev) no eixo Y. A variável irrigation_type foi representada por diferentes cores, facilitando a comparação entre os tratamentos. A função geom_jitter() foi empregada para aplicar uma leve dispersão horizontal aos pontos. As cores dos tratamentos foram definidas manualmente com scale_color_manual() e a estética do gráfico foi finalizada com theme_minimal().

# Gráficos de pontos (dados de umidade moderada)
ggplot(dados_moderate, aes(x = time, y = sev, color = irrigation_type)) +
  geom_jitter(size = 2, alpha = 0.7) +
  labs(
    title = "Severidade ao longo do tempo - Umidade Moderada",
    x = "Tempo",
    y = "Severidade",
    color = "Tipo de Irrigação"
  ) +
  scale_color_manual(values = cores_irrigation) +
  theme_minimal() +  # base limpa
  theme(
    plot.title = element_text(family = "poppins", size = 15, face = "bold", hjust = 0.5),
     plot.title.position = "plot",
    axis.title = element_text(family = "roboto", size = 12, face = "plain"),
    axis.text = element_text(family = "roboto", size = 12),
    legend.title = element_text(family = "roboto", size = 13),
    legend.text = element_text(family = "roboto", size = 10),
    legend.position = "bottom"
  )

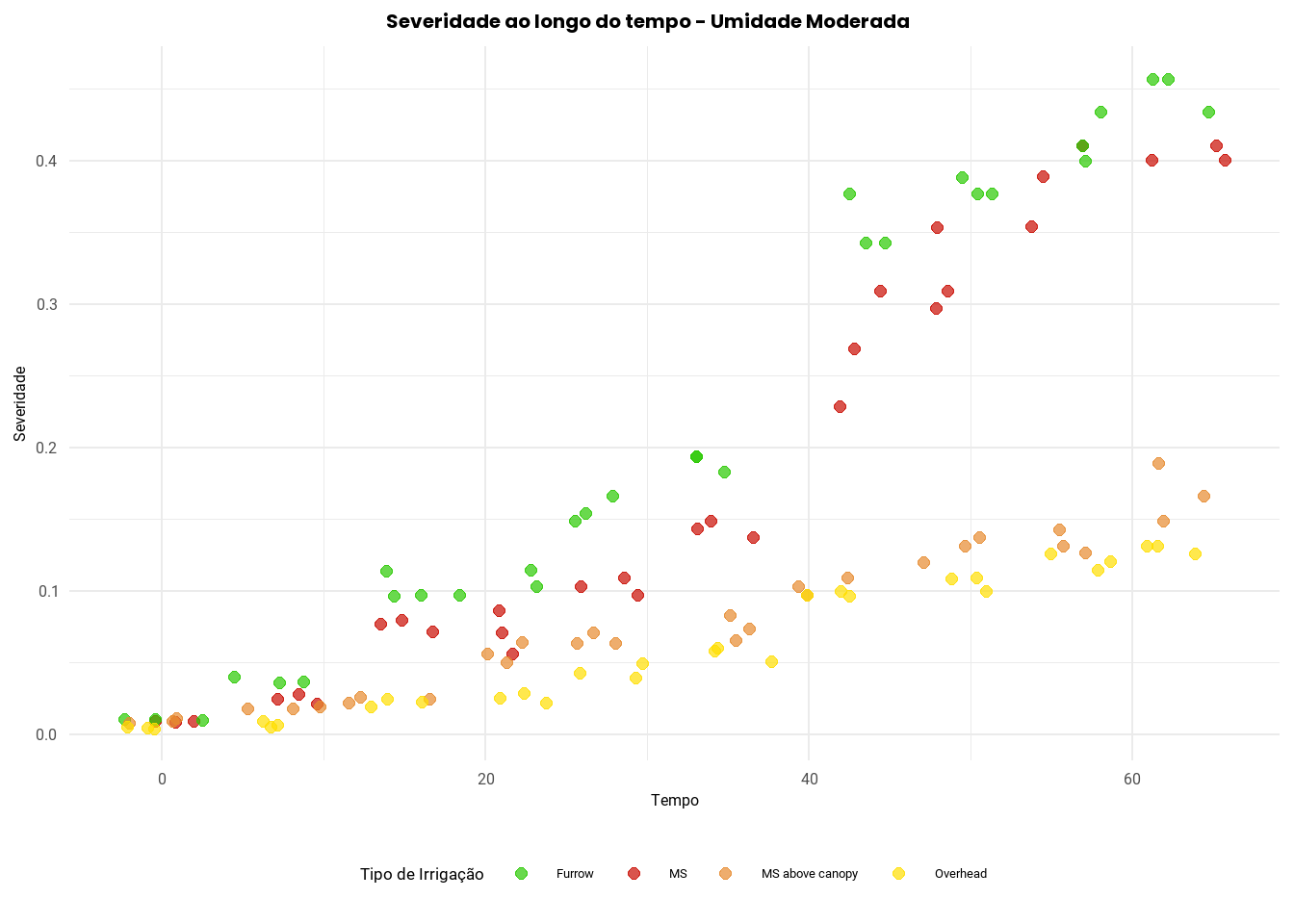
Gráfico de Severidade ao Longo do Tempo – Umidade Alta

Para a condição de umidade alta, foi construído um gráfico semelhante, utilizando o conjunto dados_high.

# Gráficos de pontos (dados de umidade alta)
ggplot(dados_high, aes(x = time, y = sev, color = irrigation_type)) +
  geom_jitter(size = 2, alpha = 0.7) +
  labs(
    title = "Severidade ao longo do tempo - Umidade Alta",
    x = "Tempo",
    y = "Severidade",
    color = "Tipo de Irrigação"
  ) +
  scale_color_manual(values = cores_irrigation) +
  theme_minimal() +  # base limpa
  theme(
    plot.title = element_text(family = "poppins", size = 15, face = "bold", hjust = 0.5),
     plot.title.position = "plot",
    axis.title = element_text(family = "roboto", size = 12, face = "plain"),
    axis.text = element_text(family = "roboto", size = 12),
    legend.title = element_text(family = "roboto", size = 13),
    legend.text = element_text(family = "roboto", size = 10),
    legend.position = "bottom"
  )

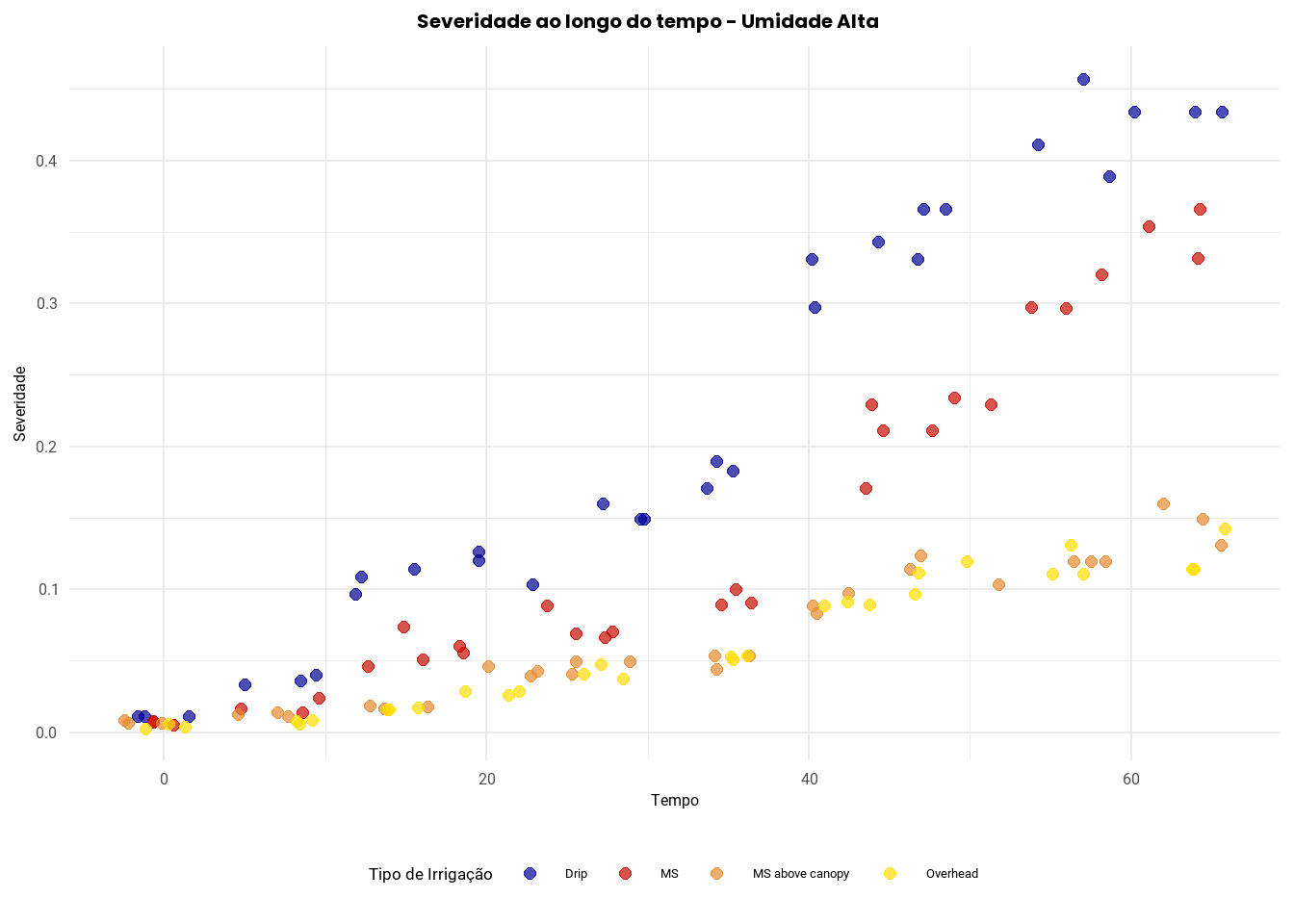
Gráfico de pontos e linhas

Antes da construção do gráfico, os dados foram agrupados pelas variáveis tratamento (combinação de tipo de irrigação + umidade), e time (tempo de avaliação). Em seguida, foi calculada a média da severidade (sev_mean) e o desvio padrão (sev_sd) para cada grupo. Ambas as métricas foram multiplicadas por 100 para expressar os valores em percentual:

O gráfico foi gerado com base no objeto dados3, contendo os valores médios e as respectivas variações da severidade. Os principais elementos visuais são: Linhas (geom_line): mostram a evolução média da severidade ao longo do tempo para cada tratamento. Pontos (geom_point): indicam os valores médios pontuais, com o preenchimento colorido conforme o tratamento. Barras de erro (geom_errorbar): representam a variação (± desvio padrão) em torno da média, permitindo avaliar a dispersão dos dados.

Preparação e agregação dos dados

Utilizou-se a função mutate() para criar uma nova variável chamada “tratamento”, que combina os fatores tipo de irrigação (irrigation_type) e nível de umidade do solo (moisture) em uma única coluna, separadas por ” + “.

Além disso, a variável irrigation_type foi convertida para fator, permitindo seu uso na definição das cores dos gráficos.

Em seguida, os dados foram agregados com group_by(). Com summarise(), foram calculadas: A média da severidade da doença (sev_mean), expressa em porcentagem. O desvio padrão da severidade (sev_sd), também em porcentagem.

Esses valores foram reunidos em um novo conjunto de dados (dados3) que serviu de base para a construção de gráficos de tendência com barras de erro, permitindo a visualização da evolução da severidade da doença ao longo do tempo, com comparação entre os diferentes tratamentos.

#ALTERAÇÃO DE DADOS
dados2 <- dados %>%
  mutate(
    tratamento = paste(irrigation_type, moisture, sep = " + "),  # >>> coluna usada no eixo x
    irrigation_type = as.factor(irrigation_type)  # >>> usada para definir as cores
  )

dados3 <- dados2 %>% 
  group_by(tratamento, irrigation_type, moisture, time) %>%
  summarise(
    sev_mean = mean(sev, na.rm = TRUE) * 100,
    sev_sd = sd(sev, na.rm = TRUE) * 100
  )

Gráfico de pontos e linhas para severidade moderada

# Gráfico para Moderate moisture
ggplot(
  dados3 %>% filter(moisture == "Moderate moisture"),
  aes(x = time, y = sev_mean, color = irrigation_type, fill = irrigation_type)
) +
  geom_line(aes(group = tratamento), size = 1) +
  geom_point(shape = 21, size = 2, color = "black") +
  geom_errorbar(aes(ymin = sev_mean - sev_sd, ymax = sev_mean + sev_sd),
                width = 0, alpha = 1) +
  theme_bw() +
  theme(
    plot.title = element_text(family = "poppins", size = 15, face = "bold", hjust = 0.5),
    plot.title.position = "plot",
    axis.title = element_text(family = "roboto", size = 12, face = "plain"),
    axis.text.x = element_text(family = "roboto", size = 11),  # alterado para mostrar texto ao invés de blank
    axis.text.y = element_text(family = "roboto", size = 12),
    legend.title = element_text(family = "roboto", size = 13),
    legend.text = element_text(family = "roboto", size = 10),
    legend.position = "bottom"
  ) +
  labs(
    title = "Severidade da doença - Umidade Moderada",
    x = "Tempo (dias)",
    y = "Disease severity (%)",
    color = "Tipo de irrigação",
    fill = "Tipo de irrigação"
  ) +
  scale_color_manual(values = cores_irrigation) +
  scale_fill_manual(values = cores_irrigation)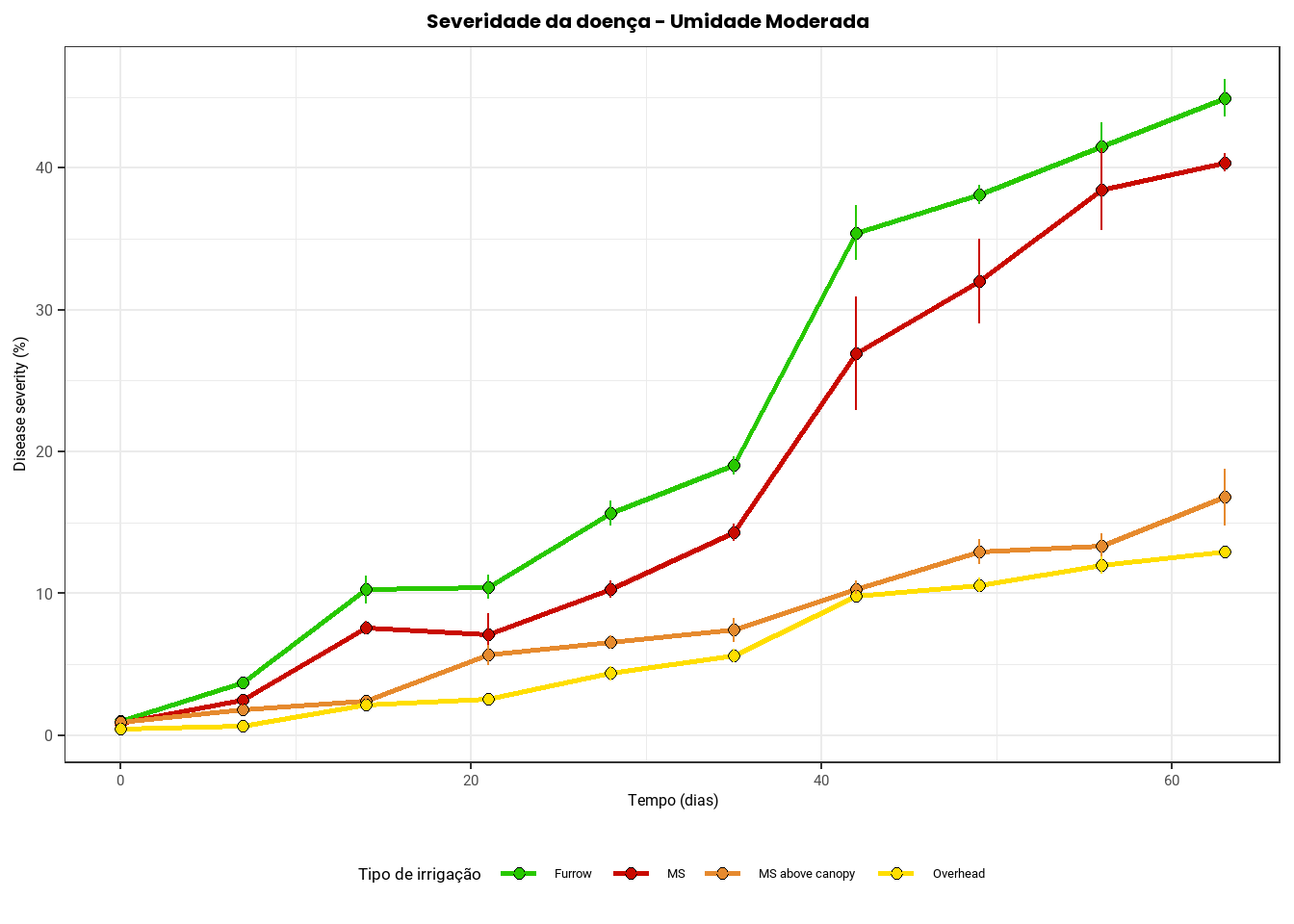

Gráfico de pontos e linhas para severidade alta

# Gráfico para high moisture
ggplot(
  dados3 %>% filter(moisture == "High moisture"),
  aes(x = time, y = sev_mean, color = irrigation_type, fill = irrigation_type)
) +
  geom_line(aes(group = tratamento), size = 1) +
  geom_point(shape = 21, size = 2, color = "black") +  # fill é mapeado, contorno preto fixo
  geom_errorbar(aes(ymin = sev_mean - sev_sd, ymax = sev_mean + sev_sd),
                width = 0, alpha = 1) +
 theme_bw() +
  theme(
    plot.title = element_text(family = "poppins", size = 15, face = "bold", hjust = 0.5),
    plot.title.position = "plot",
    axis.title = element_text(family = "roboto", size = 12, face = "plain"),
    axis.text.x = element_text(family = "roboto", size = 11),  # alterado para mostrar texto ao invés de blank
    axis.text.y = element_text(family = "roboto", size = 12),
    legend.title = element_text(family = "roboto", size = 13),
    legend.text = element_text(family = "roboto", size = 10),
    legend.position = "bottom"
  )+
  labs(
    title = "Severidade da doença - Alta Umidade",
    x = "Tempo (dias)",
    y = "Disease severity (%)",
    color = "Tipo de irrigação",
    fill = "Tipo de irrigação"
  ) +
  scale_color_manual(values = cores_irrigation) +
  scale_fill_manual(values = cores_irrigation)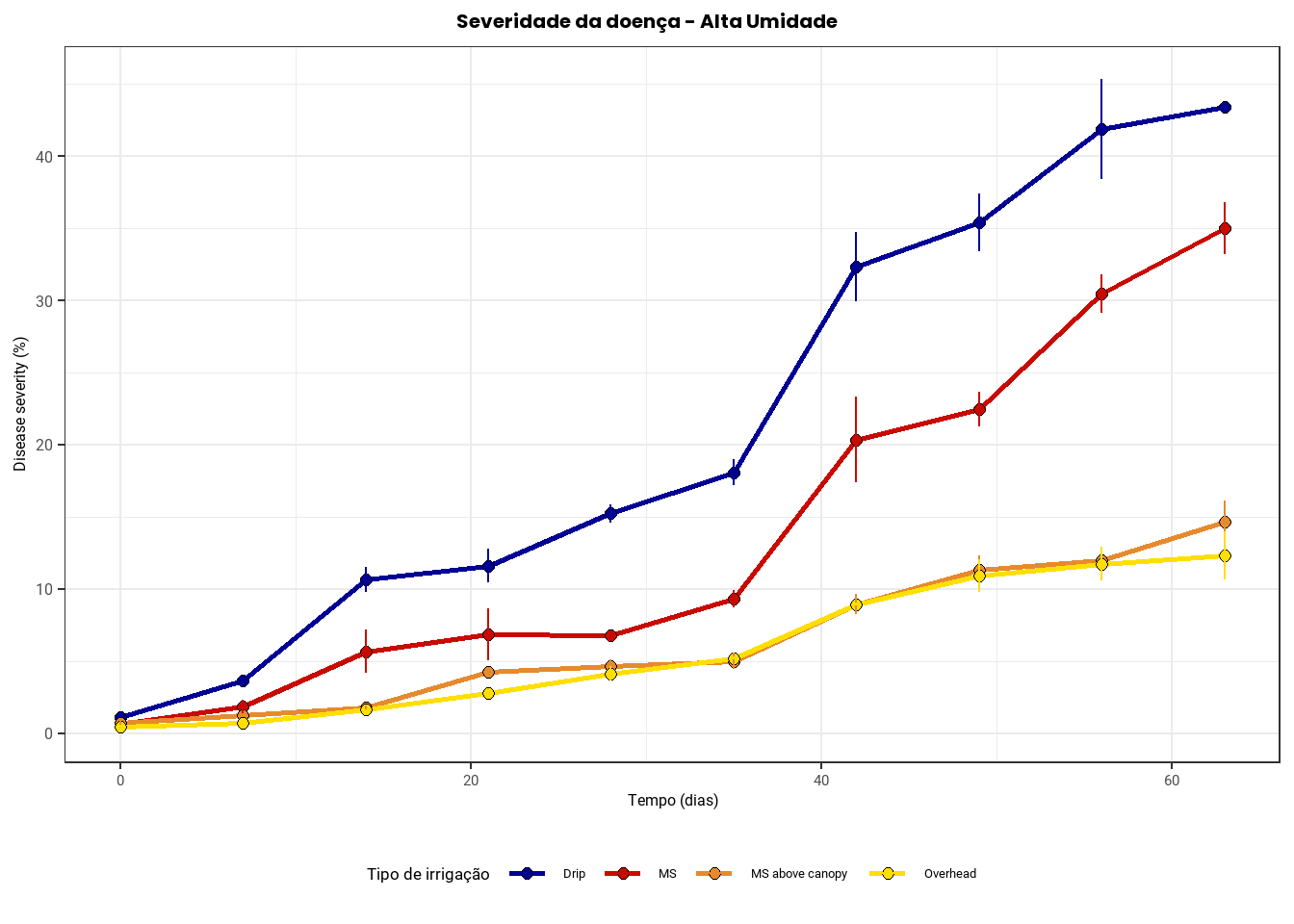

Gráfico de pontos e linhas animado

Foram criadas animações para ilustrar a evolução da severidade da doença ao longo do tempo sob condição específicas de solo, considerando os diferentes tipos de irrigação avaliados no experimento.

Para isso, os dados foram filtrados de forma a incluir apenas as observações com umidade classificada como “moderate moisture” em um gráfico e “high moisture” no outro. Em seguida, utilizou-se o pacote ggplot2 para construir o gráfico.

A animação foi gerada com a função animate() do pacote gganimate, com taxa de 10 quadros por segundo, resolução de 800x500 pixels e salvo como arquivo .gif nomeado “severidade_[moisture_level]_moisture.gif”.

Essa visualização dinâmica permite observar de forma clara como a severidade da doença evolui ao longo do tempo sob diferentes tipos de irrigação.

Umidade moderada

gif_moderate <- ggplot(
  dados3 %>% filter(moisture == "Moderate moisture"),
  aes(x = time, y = sev_mean, color = irrigation_type, fill = irrigation_type)
) +
  geom_line(aes(group = tratamento), linewidth = 1) +
  geom_point(shape = 21, size = 2, color = "black") +
  geom_errorbar(
    aes(ymin = sev_mean - sev_sd, ymax = sev_mean + sev_sd),
    width = 0.2, alpha = 0.8
  ) +
  theme_bw() +
  theme(
    plot.title = element_text(family = "poppins", size = 15, face = "bold", hjust = 0.5),
    axis.title = element_text(family = "roboto", size = 12),
    axis.text = element_text(family = "roboto", size = 11),
    legend.title = element_text(family = "roboto", size = 13),
    legend.text = element_text(family = "roboto", size = 10),
    legend.position = "bottom"
  ) +
  labs(
    title = "Umidade Moderada — Dia: {frame_along}",
    x = "Tempo (dias)",
    y = "Severidade da doença (%)",
    color = "Tipo de irrigação",
    fill = "Tipo de irrigação"
  ) +
  scale_color_manual(values = cores_irrigation) +
  scale_fill_manual(values = cores_irrigation) +
  transition_reveal(along = time)

#gif_anim_moderate <- animate(gif_moderate, fps = 10, width = 800, height = 500, renderer = #gifski_renderer())
#anim_save("severidade_moderate_moisture.gif", gif_anim_moderate)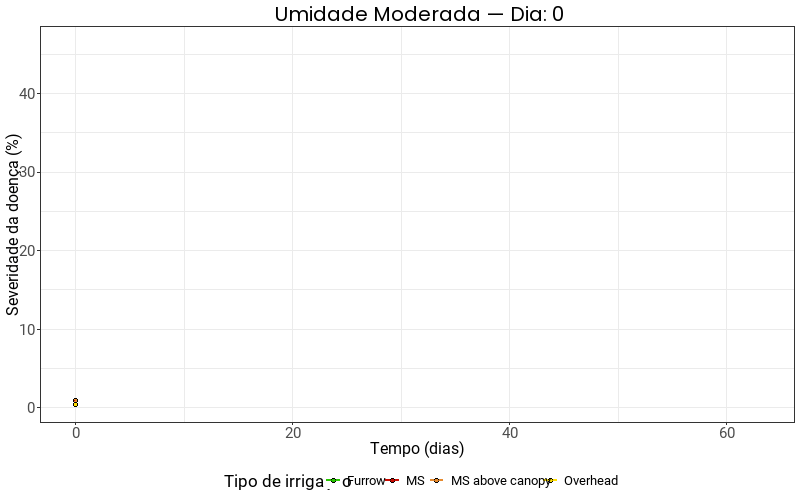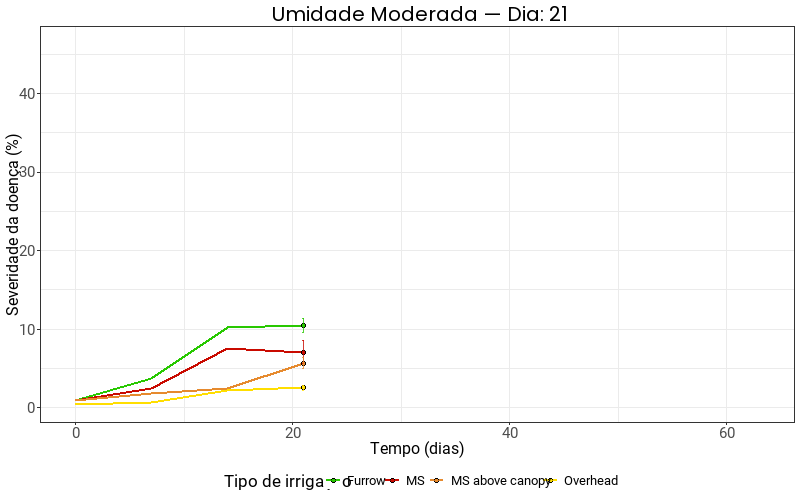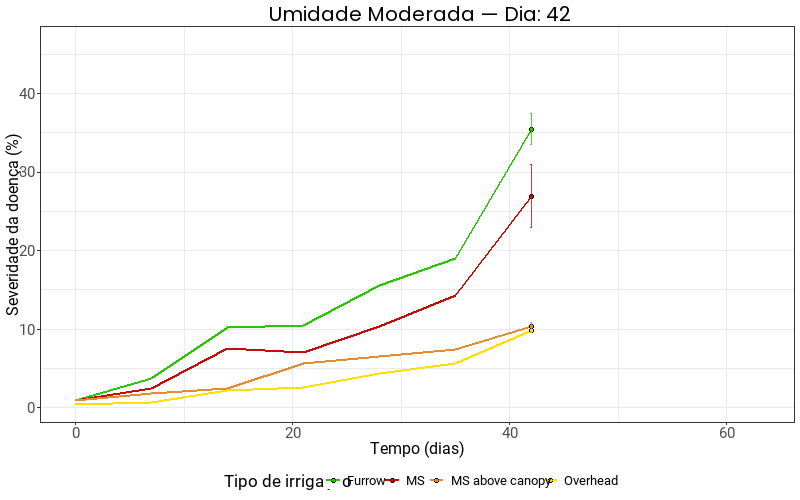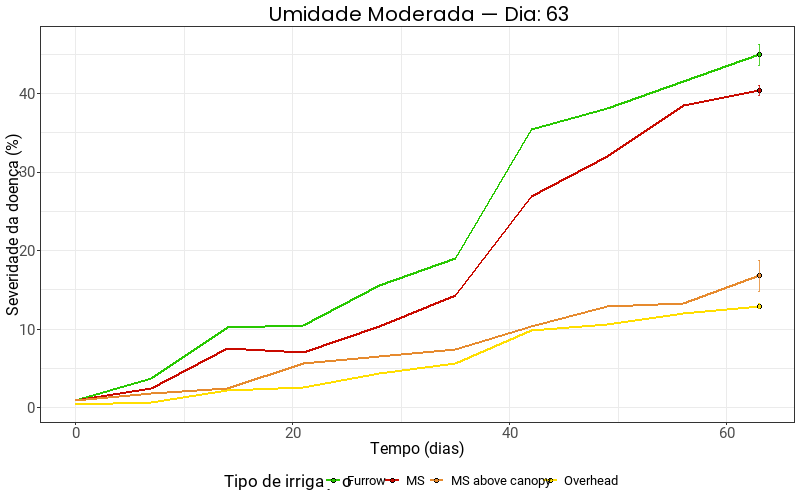

Umidade alta

gif_high <- ggplot(
  dados3 %>% filter(moisture == "High moisture"),
  aes(x = time, y = sev_mean, color = irrigation_type, fill = irrigation_type)
) +
  geom_line(aes(group = tratamento), linewidth = 1) +
  geom_point(shape = 21, size = 2, color = "black") +
  geom_errorbar(
    aes(ymin = sev_mean - sev_sd, ymax = sev_mean + sev_sd),
    width = 0.2, alpha = 0.8
  ) +
  theme_bw() +
  theme(
    plot.title = element_text(family = "poppins", size = 15, face = "bold", hjust = 0.5),
    axis.title = element_text(family = "roboto", size = 12),
    axis.text = element_text(family = "roboto", size = 11),
    legend.title = element_text(family = "roboto", size = 13),
    legend.text = element_text(family = "roboto", size = 10),
    legend.position = "bottom"
  ) +
  labs(
    title = "Alta Umidade — Dia: {frame_along}",
    x = "Tempo (dias)",
    y = "Severidade da doença (%)",
    color = "Tipo de irrigação",
    fill = "Tipo de irrigação"
  ) +
  scale_color_manual(values = cores_irrigation) +
  scale_fill_manual(values = cores_irrigation) +
  transition_reveal(along = time)

#Criar animação
#gif_anim_high <- animate(gif_high, fps = 10, width = 800, height = 500, renderer = #gifski_renderer())

# Salvar
#anim_save("severidade_high_moisture.gif", gif_anim_high)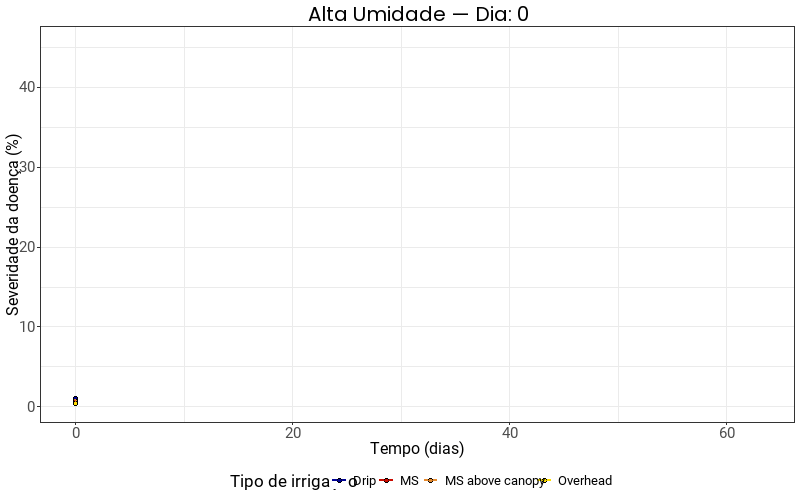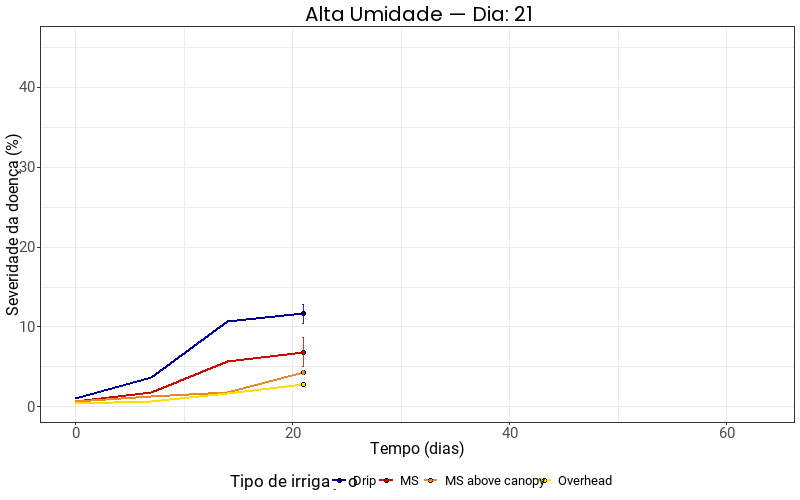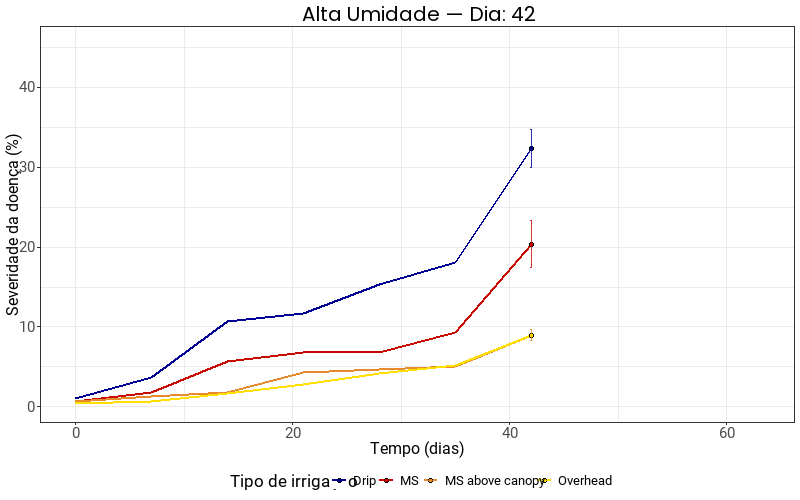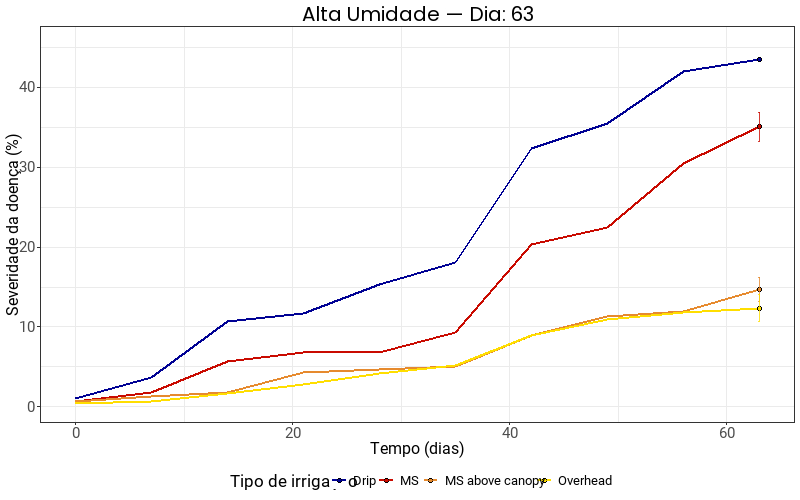

Observações:

Neste estudo, foram avaliados cinco tipos de irrigação sob dois níveis de umidade do solo: High (alta) e Moderate (moderada). No entanto, o experimento não segue um delineamento fatorial completo, ou seja, nem todos os tipos de irrigação possuem dados para ambos os níveis de umidade.

Mais especificamente:

O sistema de irrigação Drip possui dados apenas sob condição de alta umidade (High), não havendo registros para umidade moderada;
Por outro lado, o sistema Furrow está representado apenas sob umidade moderada (Moderate), sem dados disponíveis para alta umidade.

Devido a essas lacunas no delineamento, optamos por remover as combinações incompletas. Como consequência, os tratamentos “Drip” (alta umidade) e “Furrow” (umidade moderada) foram excluídos da análise, uma vez que não permitem a comparação entre os dois níveis de umidade. Essa decisão teve como objetivo garantir uma análise da interação entre os métodos de irrigação sob diferentes condições de umidade.

# Identificar quais irrigation_type têm os dois níveis de moisture
tipos_validos <- dados %>%
  group_by(irrigation_type) %>%
  summarise(n_moisture = n_distinct(moisture)) %>%
  filter(n_moisture == 2) %>%
  pull(irrigation_type)

# Filtrar os dados para manter apenas os tipos válidos
dados_filtrados <- dados %>%
  filter(irrigation_type %in% tipos_validos)

Boxplot de severidade final

Filtra o conjunto dados_filtrados para manter apenas as observações no tempo 63, considerado como tempo final de avaliação da severidade.

dados_63 <- dados_filtrados |> 
  dplyr::filter(time == 63)

Após visualizar a severidade com todos os tempos de avaliação, selecionou-se apenas a severidade final para plotar em um boxplot.

ggplot(dados_63, aes(x = irrigation_type, y = sev, fill = irrigation_type, color = irrigation_type)) +
  geom_boxplot(alpha = 0.8, size = 0.8, show.legend = FALSE) +
  labs(
    title = "Severidade por Tipo de Irrigação e Umidade",
    x = NULL,  # >>> remove o título do eixo X
    y = "Severidade",
    fill = "Tipo de Irrigação",  # >>> legenda mais limpa
    color = "Tipo de Irrigação"
  ) +
  geom_jitter(shape = 1, size = 1) +
  scale_fill_manual(values = cores_irrigation) +  # >>> novas cores por tipo
  scale_color_manual(values = cores_contorno) +      # >>> novos contornos por tipo
  facet_wrap(~moisture) +
  theme_minimal() +
  theme(
    plot.title = element_text(family = "poppins", size = 15, face = "bold", hjust = 0.5),
    plot.title.position = "plot",
    axis.title = element_text(family = "roboto", size = 12, face = "plain"),
    axis.text.x = element_blank(),  # >>> inclinação para visualização melhor
    axis.text.y = element_text(family = "roboto", size = 12),
    legend.title = element_text(family = "roboto", size = 13),
    legend.text = element_text(family = "roboto", size = 10),  # >>> aumento da fonte para melhor leitura
    legend.position = "bottom"
  ) +
guides(
  fill = guide_legend(override.aes = list(shape = 21, size = 5))
)

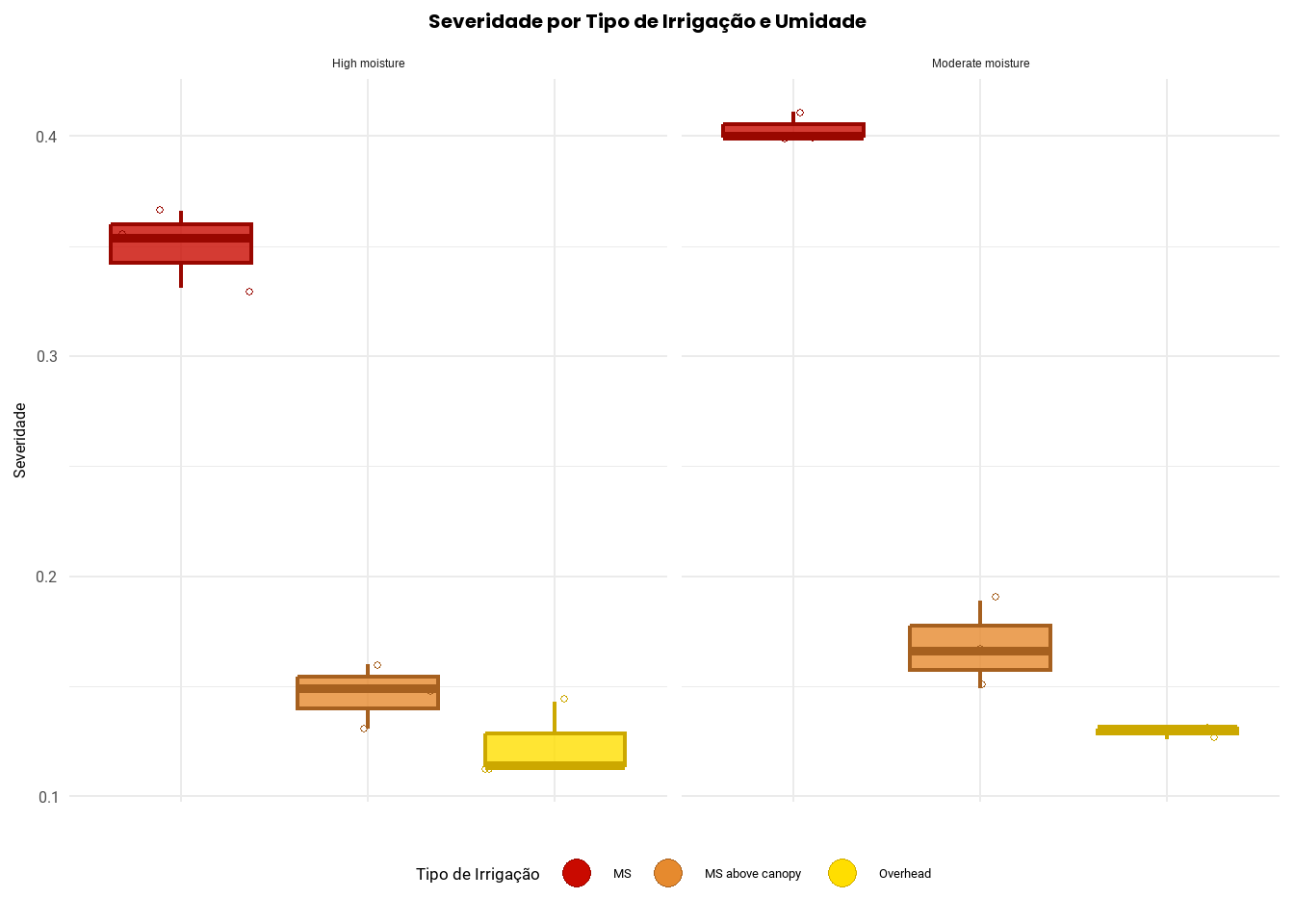
Alta umidade (High moisture)
- O tratamento MS apresenta a maior severidade média e também uma distribuição mais compacta, indicando que os valores são consistentemente altos nesse tratamento, sem muita variação entre repetições;
- O tratamento MS above canopy apresenta nível intermediário de severidade, com uma faixa mais ampla de variação entre os dados, mas ainda abaixo do MS;
- O tratamento Overhead apresenta a menor severidade, com valores mais baixos e relativamente homogêneos, sugerindo uma eficiência maior no controle da doença sob alta umidade.
Umidade moderada (Moderate moisture)
- A severidade permanece alta no tratamento MS, indicando que esse sistema de irrigação favorece o desenvolvimento da doença independentemente da umidade;
- O tratamento MS above canopy novamente ocupa uma posição intermediária;
- O tratamento Overhead continua sendo o mais eficaz, com a menor severidade registrada, inclusive com menor variabilidade. ## Análise estatística e teste de hipóteses
Hipótese nula (H₀): A severidade da doença é igual para todos os tratamentos estudados;
Hipótese alternativa (Hₐ): Pelo menos um dos tratamentos apresenta severidade média diferente da dos demais.

ANOVA

Para a realização da ANOVA, foi considerado apenas o último tempo de avaliação da severidade da doença (aos 63 dias de avaliação), uma vez que o objetivo principal era identificar quais tratamentos apresentaram menor severidade e, portanto, foram mais eficazes no controle da doença. A análise foi conduzida para avaliar os efeitos do tipo de irrigação (irrigation_type), do nível de umidade do solo (moisture) e de sua interação (irrigation_type × moisture). O bloco experimental (block) foi incluído como fator aleatório, convertido com as.factor(block).

A análise do modelo de ANOVA foi realizada utilizando a função aov, a qual faz parte do pacote base do R. Os resultados da ANOVA foram obtidos com summary(aov_dados63), permitindo a identificação de efeitos significativos entre os tratamentos.

aov_dados63 = aov(sev ~ irrigation_type*moisture + as.factor(block), data = dados_63)
summary(aov_dados63)

                         Df  Sum Sq Mean Sq F value   Pr(>F)    
irrigation_type           2 0.22391 0.11195 462.898 1.39e-10 ***
moisture                  1 0.00323 0.00323  13.342  0.00444 ** 
as.factor(block)          2 0.00011 0.00005   0.221  0.80572    
irrigation_type:moisture  2 0.00177 0.00089   3.661  0.06413 .  
Residuals                10 0.00242 0.00024                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Efeito	df	F value	Pr(>F)	Significância
`irrigation_type`	2	462.898	1.39e-10	*** significativo ao nível de 0%
`moisture`	1	13.342	0.00444	** significativo ao nível de 0,1%
`block` (como fator)	2	0.221	0.80572	NS
`irrigation_type:moisture`	2	3.661	0.06413	. significativo ao nível de 10%
`residual`	10	—	—	—

A hipótese nula (H₀) foi rejeitada, uma vez que os valores de p para os fatores principais foram menores que ao nível de significância de 0,05. Assim, aceita-se a hipótese alternativa (Hₐ), indicando que pelo menos um dos tratamentos difere significativamente dos demais.

Efeito principal de tipo de irrigação (irrigation_type):
Muito significativo (p < 0,001), indicando que os diferentes métodos de irrigação afetaram de forma clara e consistente a severidade da doença;
Efeito principal de umidade (moisture):
Significativo (p = 0,00444), sugerindo que o nível de umidade do solo (alta vs. moderada) também teve impacto importante na severidade da doença, independentemente do tipo de irrigação;
Efeito do bloco (block):
Não significativo (p = 0,80572), indicando que a variação entre blocos foi mínima, o que pode ser interpretado como consistência entre repetições;
Interação entre irrigação e umidade (irrigation_type:moisture): Marginalmente significativa (p = 0,06413), a interação entre os fatores sugere que o efeito da umidade pode depender do tipo de irrigação, embora não tenha atingido significância estatística ao nível de 5%.

Checagem das premissas

Histograma

Para verificar a normalidade dos resíduos do modelo de ANOVA, foi construído um histograma dos resíduos utilizando a função hist(). O comando residuals(aov_dados63) extrai os resíduos do modelo.

# Histogram
hist(residuals(aov_dados63),
     main = "Histograma dos resíduos da ANOVA (SEV)",
     xlab = "Resíduos",
     ylab = "Frequência",
     col = "lightgreen",
     border = "black")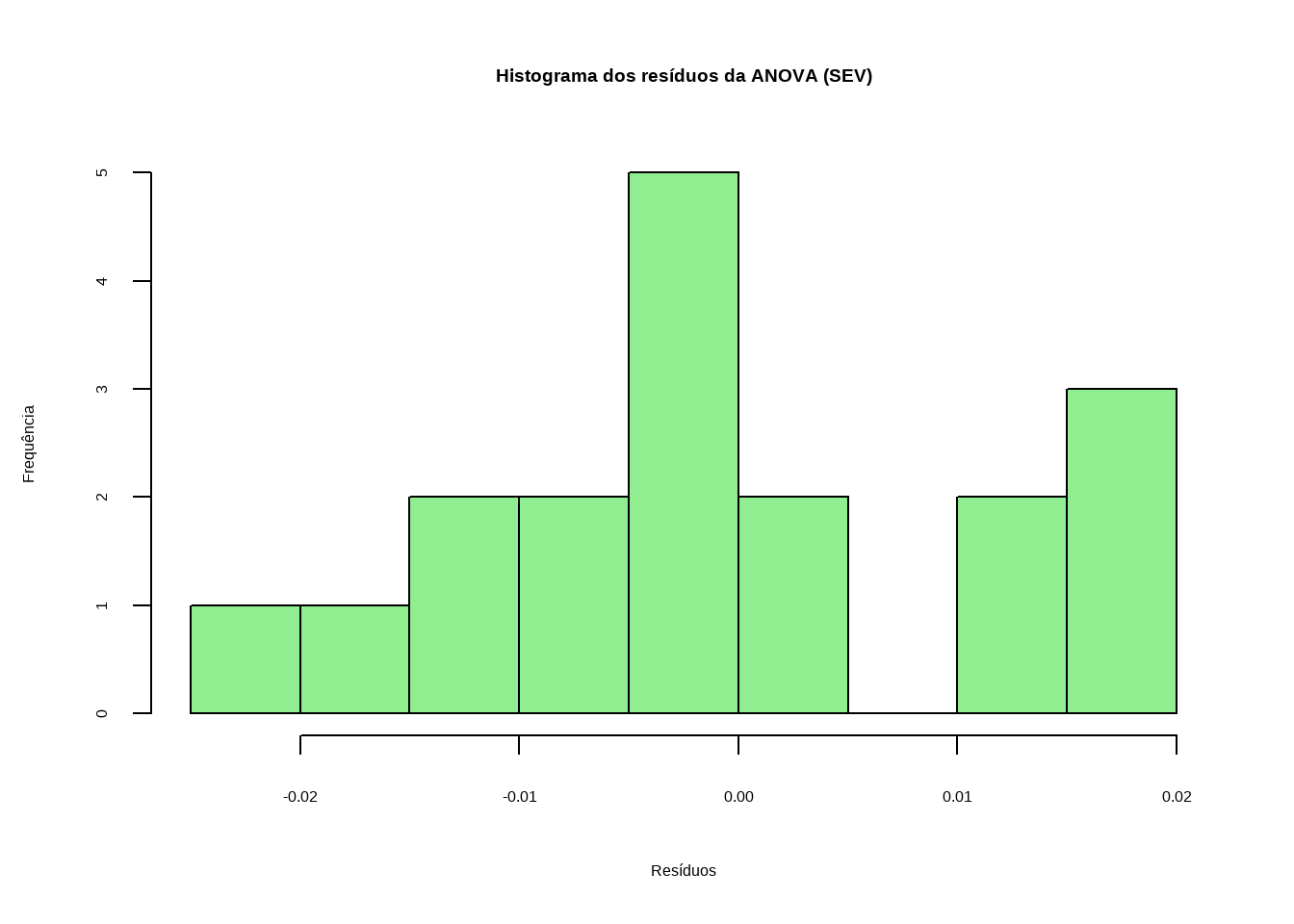

Interpretação

Forma aproximadamente simétrica: a distribuição dos resíduos é centrada em torno de zero, o que é um indicativo positivo de normalidade. Os resíduos estão distribuídos em um intervalo relativamente estreito (aproximadamente entre -0,025 e 0,02), sugerindo ausência de valores extremos (outliers).

DHARMa

Para avaliar as suposições do modelo linear ajustado, foi utilizada a simulação de resíduos por meio do pacote DHARMa.

Primeiramente, foi ajustado um modelo linear aos dados. Em seguida, os resíduos foram simulados com a função simulateResiduals() do pacote DHARMa, que gera resíduos padronizados baseados em simulações sob o modelo ajustado. Essa abordagem é especialmente útil para detectar desvios de normalidade, heterocedasticidade e efeitos de estrutura nos dados.

modelo_lm <- lm(sev ~ irrigation_type * moisture + as.factor(block), data = dados_63)

# 4. Simular resíduos com DHARMa
residuos_sim <- simulateResiduals(fittedModel = modelo_lm)

# 5. Plotar diagnósticos
plot(residuos_sim)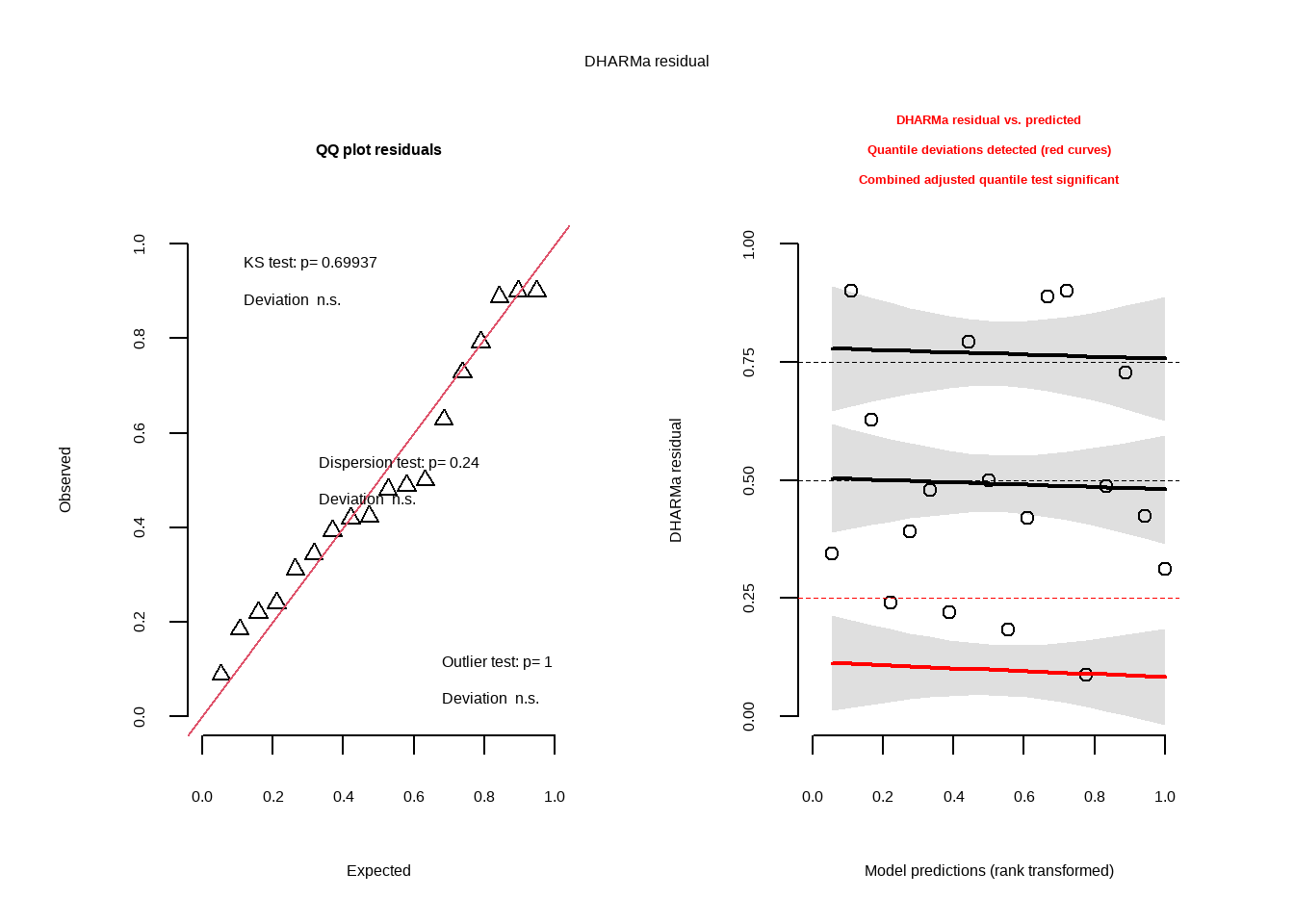

Painel esquerdo - QQ-plot dos resíduos simulados:

Esse gráfico demonstra a normalidade dos resíduos de forma robusta.

Os triângulos seguem bem a linha vermelha de 45°, o que é um bom sinal.

KS test: p = 0.69937, maior que p > 0.05. Não há evidência de que os resíduos violam a normalidade.

Dispersion test: p = 0.24. Não há problema de superdispersão.

Outlier test: p = 1. Nenhum outlier significativo detectado.

Os resíduos estão aproximadamente normais e sem outliers problemáticos. Pressuposto de normalidade atendido.

Painel Direito - Resíduos simulados vs valores preditos

O que o gráfico indica:

Red curves: significância estatística - a presença de curvas vermelhas indica que houve desvio significativo dos quantis esperados.

O texto vermelho confirma: Isso não é um problema grave, mas sugere que:

Pode haver algum padrão residual leve, talvez relacionado a variâncias diferentes entre grupos (heterocedasticidade leve);
Isso não invalida o modelo, mas é um sinal para cautela na interpretação dos efeitos;
Por isso, foi realizado o leveneTest() para confirmar se há heterocedasticidade.

Depois foram utilizados testes mais específicos para verificar a normalidade:

Normalidade

Primeiramente, utilizou-se a função check_normality() para obter uma verificação geral da normalidade dos resíduos.

Em seguida, foi construído um gráfico QQ-plot (Quantile-Quantile). Esse gráfico compara a distribuição dos resíduos observados com a distribuição normal teórica. Uma boa aderência dos pontos à linha vermelha indica que os resíduos seguem aproximadamente uma distribuição normal, o que foi observado no gráfico, sem desvios acentuados.

Por fim, foi aplicado o teste de Shapiro-Wilk shapiro.test(). Esse teste estatístico avalia formalmente a hipótese nula de que os resíduos seguem uma distribuição normal. Um valor de p ≥ que 0,05 indica que não há evidências para rejeitar a normalidade dos resíduos, confirmando que essa suposição foi atendida no modelo.

check_normality(aov_dados63)

OK: residuals appear as normally distributed (p = 0.369).

# QQ-plot
qqnorm(residuals(aov_dados63), main = "QQ-Plot dos resíduos") 
qqline(residuals(aov_dados63), col = "red", lwd = 2)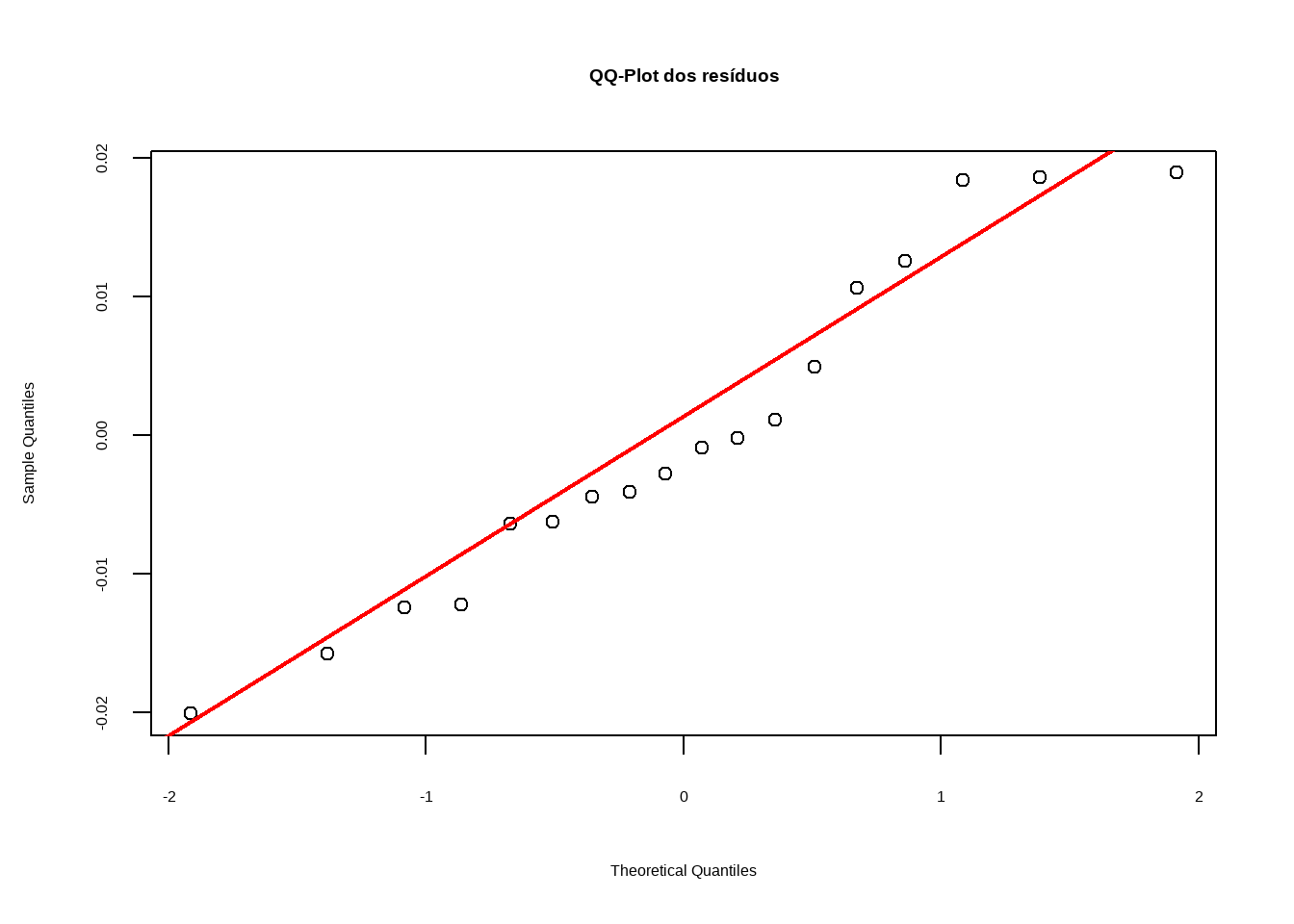

# Teste de Shapiro-Wilk
shapiro.test(residuals(aov_dados63))


    Shapiro-Wilk normality test

data:  residuals(aov_dados63)
W = 0.9462, p-value = 0.3686

Homocedasticidade

Primeiramente testou-se a homocedasticidade com a função check_heteroscedasticity().

Bartlett’s test (bartlett.test): É indicado apenas quando os resíduos seguem uma distribuição normal.

Um valor de p > 0,05 indica que não há evidência significativa de heterogeneidade de variâncias, ou seja, a suposição de homocedasticidade é atendida.

Levene’s test (leveneTest): Este teste é mais robusto quando a normalidade não pode ser totalmente garantida.
Um p > 0,05 sugere homogeneidade de variâncias entre os grupos. Se o valor for menor que 0,05, isso indicaria heterocedasticidade, violando uma das suposições da ANOVA.

check_heteroscedasticity(aov_dados63)

OK: Error variance appears to be homoscedastic (p = 0.829).

#Bartlett (apenas se resíduos forem normais):
bartlett.test(sev ~ interaction(irrigation_type, moisture), data = dados_63)


    Bartlett test of homogeneity of variances

data:  sev by interaction(irrigation_type, moisture)
Bartlett's K-squared = 5.8917, df = 5, p-value = 0.3169

#Para dados não necessariamente normais
leveneTest(sev ~ interaction(irrigation_type, moisture), data = dados_63)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  5  0.5556  0.732
      12

Teste de comparação de médias

A função emmeans() (Estimated Marginal Means) calcula as médias ajustadas — também conhecidas como médias marginais estimadas — para as combinações dos fatores irrigation_type e moisture, com base no modelo ajustado modelo_lm.

A função cld() (Compact Letter Display) agrupa os tratamentos com base nas comparações múltiplas de médias.

# Médias ajustadas
medias <- emmeans(modelo_lm, ~ irrigation_type * moisture)

# Comparações de médias com agrupamento por letras
letras <- cld(medias, adjust = "sidak", Letters = letters)

# Visualizar resultado
print(letras)

 irrigation_type moisture          emmean      SE df lower.CL upper.CL .group
 Overhead        High moisture      0.124 0.00898 10   0.0944    0.153  a    
 Overhead        Moderate moisture  0.129 0.00898 10   0.1000    0.159  a    
 MS above canopy High moisture      0.147 0.00898 10   0.1174    0.176  a    
 MS above canopy Moderate moisture  0.168 0.00898 10   0.1387    0.197  a    
 MS              High moisture      0.350 0.00898 10   0.3210    0.380   b   
 MS              Moderate moisture  0.404 0.00898 10   0.3744    0.433    c  

Results are averaged over the levels of: block 
Confidence level used: 0.95 
Conf-level adjustment: sidak method for 6 estimates 
P value adjustment: sidak method for 15 tests 
significance level used: alpha = 0.05 
NOTE: If two or more means share the same grouping symbol,
      then we cannot show them to be different.
      But we also did not show them to be the same.

As médias ajustadas foram comparadas por meio de contrastes pareados com correção de Sidak, apropriada para múltiplas comparações entre combinações de tratamentos fatoriais. Grupos com letras iguais não diferem entre si ao nível de significância de 5%.

Tipo de Irrigação	Umidade	Média Ajustada	SE	GL	IC Inferior	IC Superior	Grupo
Overhead	Alta	0.124	0.00898	10	0.0944	0.153	a
Overhead	Moderada	0.129	0.00898	10	0.1	0.159	a
MS above canopy	Alta	0.147	0.00898	10	0.1174	0.176	a
MS above canopy	Moderada	0.168	0.00898	10	0.1387	0.197	a
MS	Alta	0.35	0.00898	10	0.321	0.38	b
MS	Moderada	0.404	0.00898	10	0.3744	0.433	c

emmeans(modelo_lm, pairwise ~ moisture, adjust = "tukey")

$emmeans
 moisture          emmean      SE df lower.CL upper.CL
 High moisture      0.207 0.00518 10    0.195    0.218
 Moderate moisture  0.234 0.00518 10    0.222    0.245

Results are averaged over the levels of: irrigation_type, block 
Confidence level used: 0.95 

$contrasts
 contrast                          estimate      SE df t.ratio p.value
 High moisture - Moderate moisture  -0.0268 0.00733 10  -3.653  0.0044

Results are averaged over the levels of: irrigation_type, block

cld(emmeans(modelo_lm, ~ moisture), adjust = "tukey")

 moisture          emmean      SE df lower.CL upper.CL .group
 High moisture      0.207 0.00518 10    0.193    0.221  1    
 Moderate moisture  0.234 0.00518 10    0.220    0.247   2   

Results are averaged over the levels of: irrigation_type, block 
Confidence level used: 0.95 
Conf-level adjustment: sidak method for 2 estimates 
significance level used: alpha = 0.05 
NOTE: If two or more means share the same grouping symbol,
      then we cannot show them to be different.
      But we also did not show them to be the same.

A tabela abaixo apresenta as médias ajustadas da severidade da doença para cada nível de umidade, com erro padrão, intervalos de confiança e agrupamento por letras. O agrupamento foi realizado utilizando o método de Sidak (α = 0,05), ajustado a partir de comparações múltiplas.

Umidade	Média Ajustada	SE	GL	IC Inferior	IC Superior	Grupo
Alta	0.207	0.00518	10	0.193	0.221	1
Moderada	0.234	0.00518	10	0.22	0.247	2

AUDPC

Para quantificar o avanço da doença ao longo do tempo, foi realizada a análise da Área Abaixo da Curva de Progresso da Doença (AACPD ou AUDPC), utilizando todos os tempos de avaliação disponíveis no experimento. Essa métrica resume, em um único valor, a intensidade acumulada da doença durante o período observado, sendo amplamente utilizada em estudos epidemiológicos por refletir tanto a severidade quanto a duração da infecção.

A análise foi conduzida com o pacote epifitter (fornece funções para análise do cálculo da AACPD), especificamente por meio da função audpc(). A função audpc() calcula a Área Abaixo da Curva de Progresso da Doença com base: na severidade da doença (sev) multiplicada por 100 (para expressar em %), e no tempo de avaliação (time). O resultado é armazenado em aacpd_resultado, que contém uma linha para cada combinação de tratamento e bloco, com o valor correspondente da AACPD.

library(epifitter)
library(dplyr)

# 3. Calcular a AACPD para cada combinação de tratamento e bloco
aacpd_resultado <- dados2 %>%
  group_by(tratamento, block) %>%
  summarise(AACPD = audpc(sev*100, time), .groups = "drop")

# 4. Visualizar os resultados
print(aacpd_resultado)

# A tibble: 24 × 3
   tratamento                 block AACPD
   <chr>                      <dbl> <dbl>
 1 Drip + High moisture           1 1300.
 2 Drip + High moisture           2 1388.
 3 Drip + High moisture           3 1329.
 4 Furrow + Moderate moisture     1 1353.
 5 Furrow + Moderate moisture     2 1400.
 6 Furrow + Moderate moisture     3 1387.
 7 MS + High moisture             1  806.
 8 MS + High moisture             2  924.
 9 MS + High moisture             3  826.
10 MS + Moderate moisture         1 1052.
# ℹ 14 more rows

ANOVA

modelo_aacpd <- aov(AACPD ~ tratamento, data = aacpd_resultado)
summary(modelo_aacpd)

            Df  Sum Sq Mean Sq F value Pr(>F)    
tratamento   7 4053698  579100   400.3 <2e-16 ***
Residuals   16   23148    1447                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Checagem das premissas

Histograma

O gráfico mostrou uma distribuição aproximadamente simétrica e centrada em torno de zero, o que indica que os resíduos seguem uma tendência próxima à distribuição normal.

# Histogram
hist(residuals(modelo_aacpd),
     main = "Histograma dos resíduos da ANOVA (AACPD)",
     xlab = "Resíduos",
     ylab = "Frequência",
     col = "lightgreen",
     border = "black")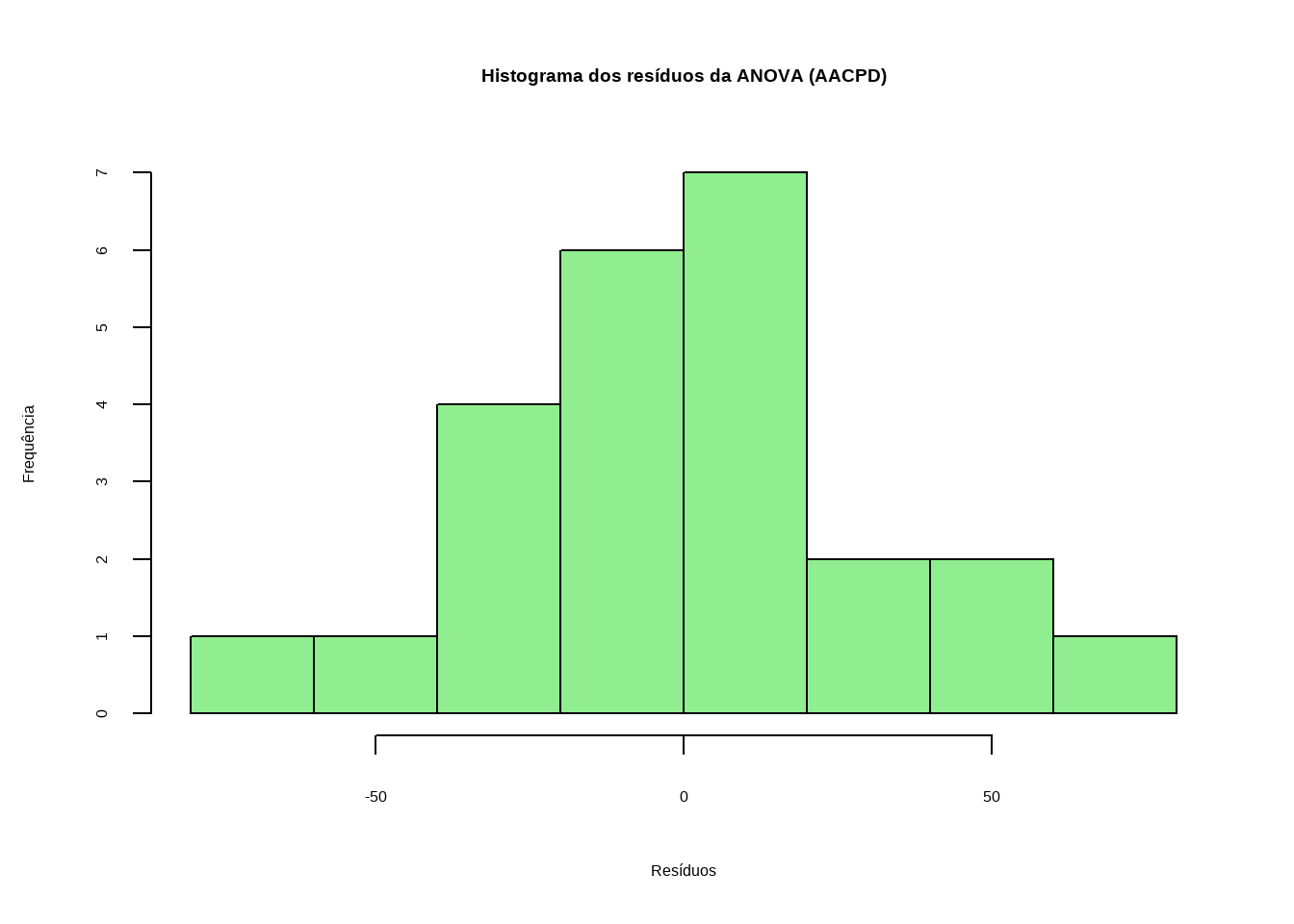

DHARMa (AACPD)

Os resultados indicaram que o modelo se comporta adequadamente, sem violações evidentes dos pressupostos estatísticos. Entretanto o resultado apresentado pelo teste de resíduos simulados vs valores preditos exige com o que seja necessário fazer testes adicionais.

modelo_lmaacpd <- lm(AACPD ~ tratamento + as.factor(block), data = aacpd_resultado)

# 4. Simular resíduos com DHARMa
residuos_simaacpd <- simulateResiduals(fittedModel = modelo_lmaacpd)

# 5. Plotar diagnósticos
plot(residuos_simaacpd)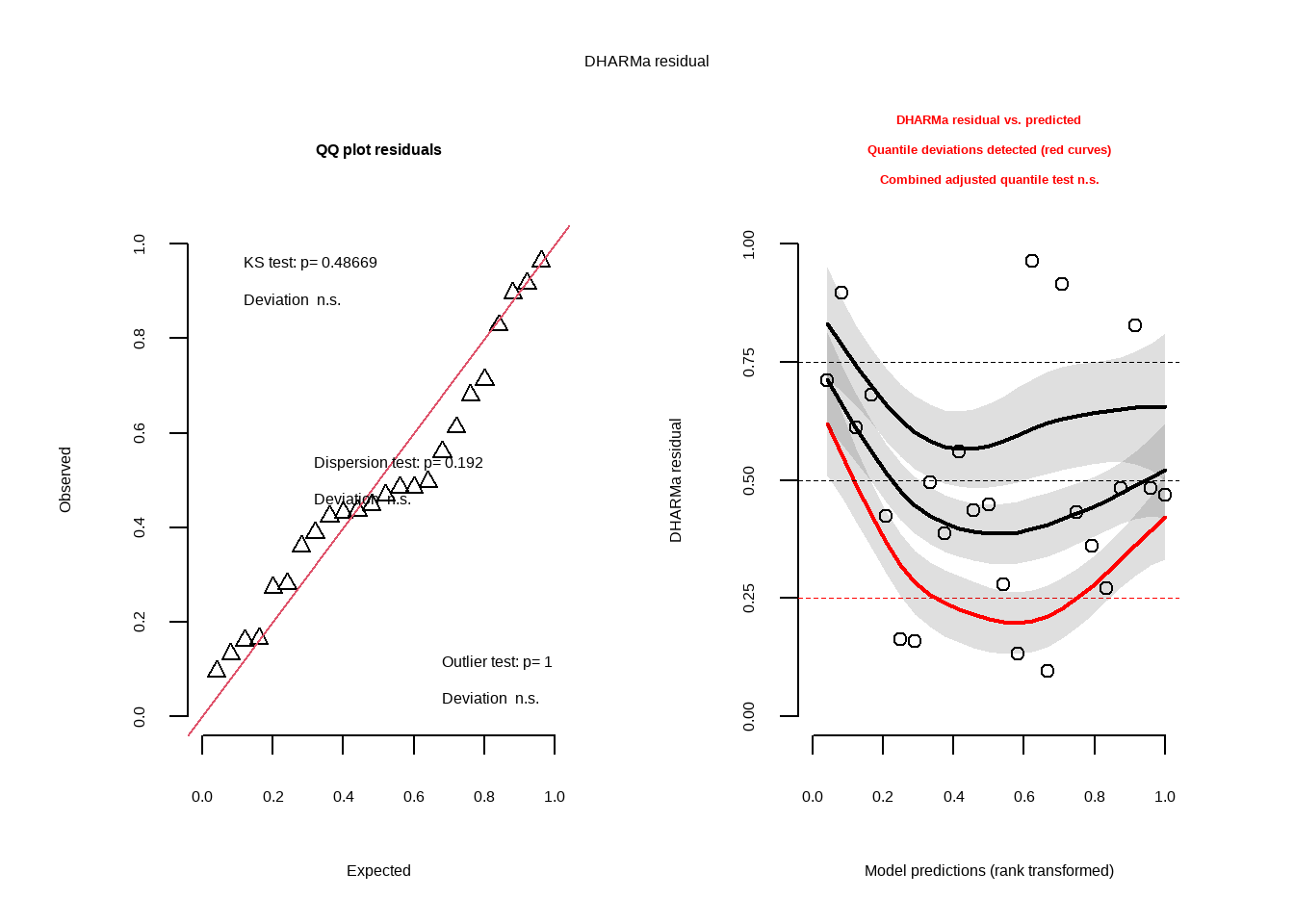

Normalidade (AACPD)

A normalidade dos resíduos do modelo de ANOVA para a variável AACPD foi avaliada por meio do gráfico QQ-Plot e do teste de Shapiro-Wilk. O gráfico indicou boa aderência dos resíduos à linha de normalidade. Já o teste de Shapiro-Wilk apresentou valor de p = 0,3125, indicando que não há evidência significativa de violação da normalidade (p > 0,05). Portanto, o modelo atende ao pressuposto de normalidade dos resíduos, sendo apropriado para a análise.

check_normality(modelo_aacpd)

OK: residuals appear as normally distributed (p = 0.972).

# QQ-plot
qqnorm(residuals(modelo_aacpd), main = "QQ-Plot dos resíduos")
qqline(residuals(modelo_aacpd), col = "red", lwd = 2)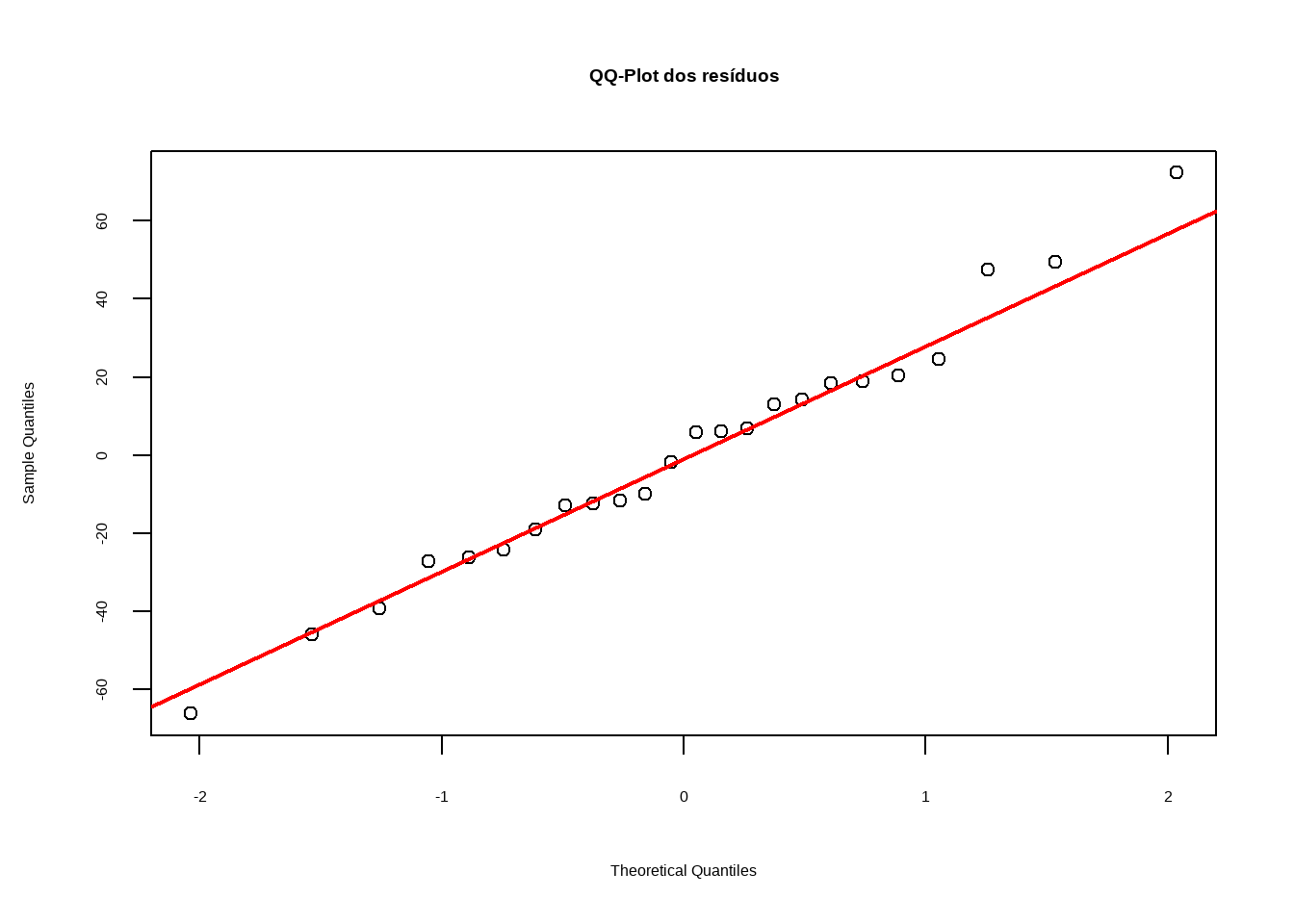

# Teste de Shapiro-Wilk
shapiro.test(residuals(modelo_aacpd))


    Shapiro-Wilk normality test

data:  residuals(modelo_aacpd)
W = 0.9855, p-value = 0.9722

Homocedasticidade (AACPD)

Esses dados confirmam a homocedasticidade dos dados, confirmando portanto a última premissa da ANOVA.

check_heteroscedasticity(modelo_aacpd)

OK: Error variance appears to be homoscedastic (p = 0.087).

#Bartlett (apenas se resíduos forem normais):
bartlett.test(AACPD ~ tratamento, data = aacpd_resultado)


    Bartlett test of homogeneity of variances

data:  AACPD by tratamento
Bartlett's K-squared = 7.7261, df = 7, p-value = 0.3574

#Para dados não necessariamente normais
leveneTest(AACPD ~ tratamento, data = aacpd_resultado)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  7  0.5639 0.7744
      16

Boxplot (AACPD)

aacpd_resultado2 <- aacpd_resultado %>%
  mutate(
    irrigation_type = case_when(
      str_detect(tratamento, "Drip") ~ "Drip",
      str_detect(tratamento, "Furrow") ~ "Furrow",
      str_detect(tratamento, "MS above canopy") ~ "MS above canopy",
      str_detect(tratamento, "MS") ~ "MS",
      str_detect(tratamento, "Overhead") ~ "Overhead"
    )
  )

aacpd_resultado2 <- aacpd_resultado2 %>%
  mutate(
    irrigation_type = case_when(
      str_detect(tratamento, "Drip") ~ "Drip",
      str_detect(tratamento, "Furrow") ~ "Furrow",
      str_detect(tratamento, "MS above canopy") ~ "MS above canopy",
      str_detect(tratamento, "MS") ~ "MS",
      str_detect(tratamento, "Overhead") ~ "Overhead"
    ),
    moisture = case_when(
      str_detect(tratamento, "High moisture") ~ "High moisture",
      str_detect(tratamento, "Moderate moisture") ~ "Moderate moisture",
      str_detect(tratamento, "Low moisture") ~ "Low moisture"
    )
  )


ggplot(aacpd_resultado2, aes(x = tratamento, y = AACPD, fill = irrigation_type, color = irrigation_type)) +
  geom_boxplot(alpha = 0.8, size = 0.8, show.legend = FALSE) +
  labs(
    title = "Área Abaixo da Curva do Progresso da Doença (AACPD)",
    x = NULL,
    y = "AACPD",
    fill = "Tipo de Irrigação",
    color = "Tipo de Irrigação"
  ) +
  geom_jitter(shape = 1, size = 1) +
  scale_fill_manual(values = cores_irrigation) +
  scale_color_manual(values = cores_contorno) +
  facet_wrap(~moisture) +
  theme_minimal() +
  theme(
    plot.title = element_text(family = "poppins", size = 15, face = "bold", hjust = 0.5),
    plot.title.position = "plot",
    axis.title = element_text(family = "roboto", size = 12, face = "plain"),
    axis.text.x = element_blank(),
    axis.text.y = element_text(family = "roboto", size = 12),
    legend.title = element_text(family = "roboto", size = 13),
    legend.text = element_text(family = "roboto", size = 10),
    legend.position = "bottom"
  ) +
  guides(
    fill = guide_legend(override.aes = list(shape = 21, size = 5))
  )

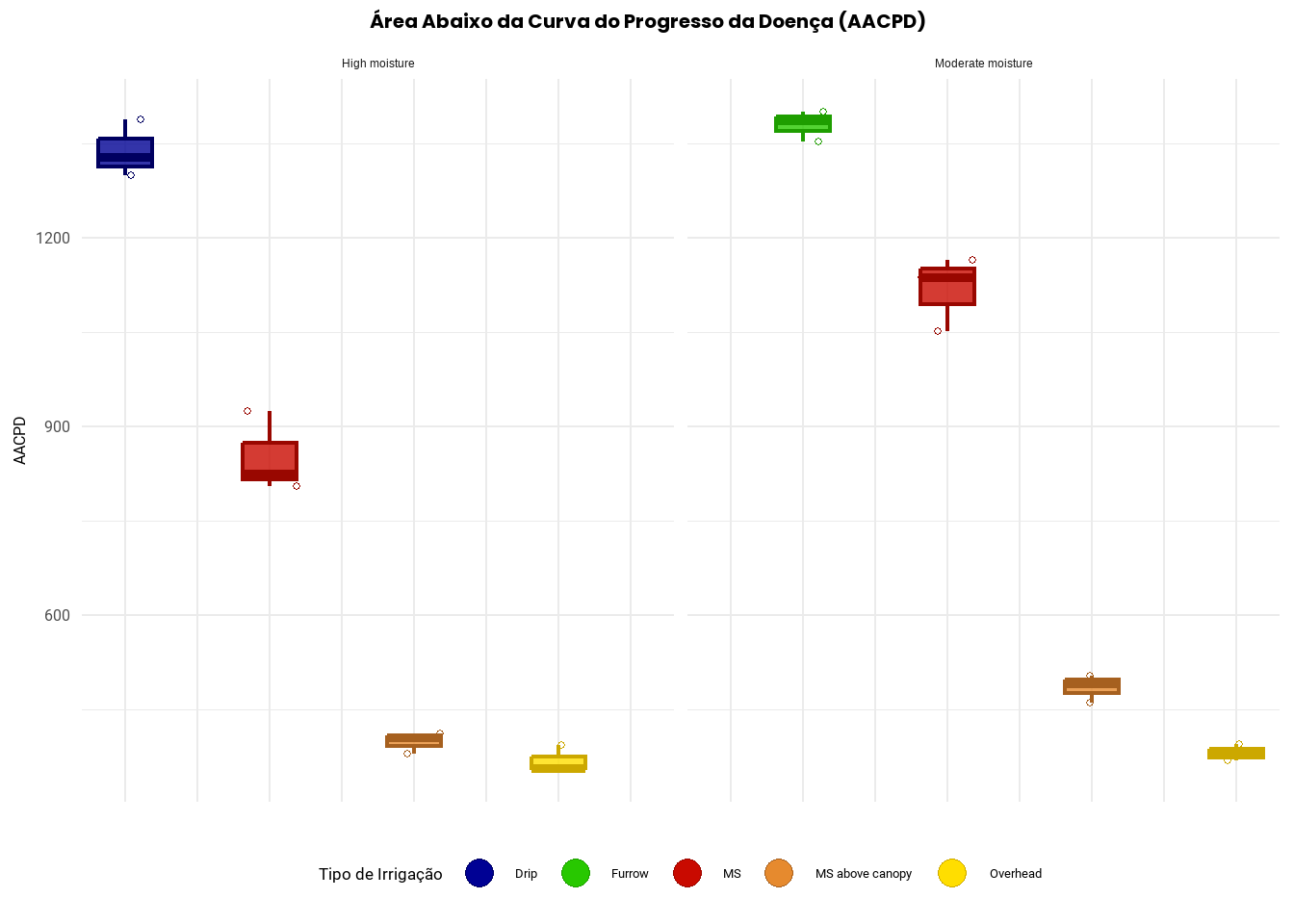
Alta Umidade (High moisture)

O Drip apresenta os maiores valores de AACPD, indicando que esse sistema favoreceu o progresso da doença sob alta umidade;
MS apresenta AACPD elevado, porém inferior ao Drip. Ainda assim, mostra que houve considerável progresso da doença;
MS above canopy apresentou AACPD baixo, sugerindo que esse método reduziu a severidade da doença em relação aos anteriores;
Overhead teve o menor AACPD, indicando a redução na severidade da doença.

Umidade Moderada (Moderate moisture)

Furrow apresenta os maiores valores de AACPD, indicando que foi o pior sistema nessa condição, com alto progresso da doença;
MS apresenta valor intermediário, sugerindo desenvolvimento significativo da doença, porém menor que no Furrow;
MS above canopy novamente mostrou bom desempenho, mantendo padrão semelhante ao observado sob alta umidade.

Teste de comparação de médias (AACPD)

# ANOVA já ajustada no objeto modelo_aacpd
# Teste de comparação de médias (Tukey)
# Converter bloco para fator, se necessário
aacpd_resultado$block <- as.factor(aacpd_resultado$block)

# Rodar ANOVA novamente com bloco (modelo mais completo)
modelo_com_bloco <- aov(AACPD ~ tratamento + block, data = aacpd_resultado)

# Teste de Tukey com agricolae
tukey_resultado <- HSD.test(modelo_com_bloco, trt = "tratamento", group = TRUE)

# Visualizar grupos
print(tukey_resultado$groups)

                                        AACPD groups
Furrow + Moderate moisture          1379.9333      a
Drip + High moisture                1338.9833      a
MS + Moderate moisture              1118.3667      b
MS + High moisture                   852.0167      c
MS above canopy + Moderate moisture  485.5667      d
MS above canopy + High moisture      399.2333     de
Overhead + Moderate moisture         381.2667      e
Overhead + High moisture             368.4333      e

A tabela abaixo apresenta as médias de AACPD e o agrupamento por letras. O agrupamento foi feito com base na comparação múltipla utilizando o método de TukeyHSD ajustado para Tukey (α = 0,05). Letras iguais indicam ausência de diferença estatística significativa.

Tratamento	Média AACPD	Grupo
Furrow + Moderate moisture	1379.93	a
Drip + High moisture	1338.98	a
MS + Moderate moisture	1118.37	b
MS + High moisture	852.02	c
MS above canopy + Moderate moisture	485.57	d
MS above canopy + High moisture	399.23	de
Overhead + Moderate moisture	381.27	e
Overhead + High moisture	368.43	e

Conclusão

Conclui‑se que o tipo de irrigação exerce influência decisiva sobre a severidade do oídio em tomateiro, de modo estatisticamente significativo. Na primeira análise, removemos os tratamentos “drip” e “furrow” para manter o experimento fatorial completo e assim testar formalmente a interação entre os fatores irrigação e umidade. Não houve interação significativa, o que indica que cada fator age de forma independente sobre a doença. Já na segunda análise, trabalhamos com valores de área sob a curva de progresso da doença (AUDPC), considerando as oito combinações de irrigação e umidade em conjunto, e submetemos esses valores a comparações de médias, também revelando diferenças estatisticamente significativas entre os tratamentos.

Do ponto de vista biológico, os sistemas que molham diretamente o dossel (aspersão aérea, “overhead”) apresentaram as menores severidades, provavelmente porque filmes de água na superfície foliar inibem a germinação e penetração dos conídios de Leveillula taurica. Em contraste, métodos que mantêm as folhas relativamente secas — gotejamento (“drip”) e sulco (“furrow”) — elevam a umidade relativa ao redor das plantas sem provocar esse “lavamento” das estruturas do fungo, criando condições ideais para seu desenvolvimento. As microaspersões no solo e acima do dossel tiveram resultados intermediários, reforçando que tanto a via de aplicação da água quanto o nível de umidade contribuem separadamente para a gravidade do oídio em tomateiro.